Answer: Are tree rings nested cones or cylinders?

  Simple questions... 

P/C Sevenstorm (from Pexels.com)

... can begin from humble circumstances and can lead to deep insights. 

In this Challenge, I saw the stump of a tree wondered if the number of growth rings near the top of the tree would be the same as the number of rings near the bottom.  I counted the rings and found that it was around 25 years old.  But then I saw another cross section of the tree, but much narrower and taken from much higher up on the trunk, a bit like this: 

THAT made me pause for a moment and wonder--if I could somehow X-ray the tree, how would the rings be arranged on the inside?  

In other words, are number of rings the same at the bottom of the tree as at the top?   

1. Are the rings in a tree trunk arranged as a cone or as a collection of cylinders?  In other words, if you count the rings at the top of the tree, would you see the same number of rings as at the bottom?  (If they're stacked cones, you'd expect the number to be different--if they're cylinders, you'd expect them to be the same.)  How ARE the tree rings organized inside of the tree trunk? 

This turns out to be more complicated than it sounds.  (See what I mean?  Even simple questions about things you see everyday can lead to unanticipated depths.)  

I was thinking of the inside of tree like this: 

Dan's sketch of a tree

And, if you took a vertical cross-section of the tree, you'd see something like one of these two sketches of the very top of the tree:

Cross section of a tree.

The question I had in mind was this: Are the tree growth rings arranged like the one on the left? (Like nesting cones stacked on top of each other.) Or more like the one on the right?  (All of the growth rings flow from a single point on top of the tree.) 

In other words, are the growth rings conical or cylindrical?  

This matters because if you cut the tree at level 1 (see above), the left tree would show only 2 rings, while the right tree would show 3 rings.  So... which is it? 

I did various versions of searches like: 

     [ tree growth rings same at top and bottom ] 

     [ are the number of tree rings the same at the top and bottom ] 

     [ are tree rings arranged in a cone or a cylinder ] 

These searches all led to Quora pages or Reddit pages, most of which disagreed with each other.  Some say the number of rings are constant from bottom to top (like cylinders) while some say the number varies from bottom to top (like stacked cones).  

I asked Bard and ChatGPT this question: 

     [ do trees have the same number of growth rings at
        the top of the tree as at the bottom of the tree?  ] 

ChatGPT:  

Yes, trees have the same number of growth rings at the top of the tree as at the bottom. Growth rings, also known as annual rings, are layers of wood produced by the tree's cambium (the layer of growing tissue) each year during its growing season. These rings indicate the age of the tree and can provide information about the environmental conditions during each year of the tree's life.

The number of growth rings is consistent throughout the entire height of the tree because the rings represent the growth of the tree in a given year, regardless of the height at which you are examining the tree. Whether you're looking at a cross-section near the base of the tree or a cross-section higher up, you will count the same number of growth rings, assuming the sections are from the same tree and the tree is healthy and growing normally.

The uniformity of growth rings throughout the tree is a result of the tree's growth process, which occurs outward from the cambium layer, encircling the entire trunk and branches. This process ensures that each year's growth is recorded as a ring around the entire circumference of the tree.

Gemini/Bard: 

Yes, trees generally have the same number of growth rings at the top as at the bottom of the tree. This is because new growth occurs at the tips of the branches and the main stem, and this new growth adds a new ring to the entire tree, from the top to the bottom. 

Imagine the tree trunk as a long, thin cylinder. As the tree grows taller, the cylinder gets longer, but its overall width stays the same. The growth rings are like the layers of paint on the cylinder, and each new layer is added on top of the previous ones, all the way from the top to the bottom.

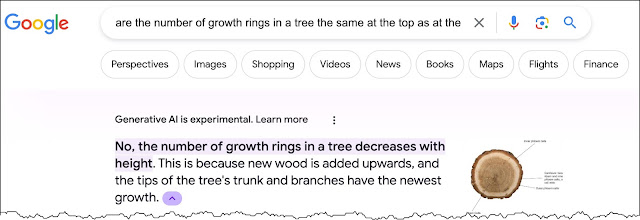
Aside from telling me that trees don't taper as they get taller (really, Gemini?), interestingly, and oddly, the Gen-AI answer feature in Google gave a different answer in the SERP than regular Gemini!  (See below. The SERP says "no," but Gemini says "yes."  What's up with that?) 

Okay... How am I going to get an authoritative answer?  

Rather than asking the LLMs, or believing the conflicting stories in Reddit and Quora, I went to Google Scholar and Google Books.  Both have pretty reliable content, most of which is peer-reviewed (or in the case of Books, at least carefully reviewed by an editor and publishing house).  

In Google Books I did: 

     [ tree ring growth same at top of tree as at the bottom ] 

and found several books of interest, but one in particular stood out.   Tree rings: timekeepers of the past. Phipps, R. L., & McGowan, J. (1993). US Department of the Interior, US Geological Survey.

In this book (published by the USGS, a reputable organization) you'll read: 

Looking down at a stump top, it may be difficult to visualize how tree rings go together to make a tree. Perhaps this is because a tree is a three-dimensional object and a stump top displays only two dimensions. The idea of three-dimensional growth can be clarified, however, by disregarding for the moment the leaves, branches, roots, and bark, and considering only the wood portion of the tree trunk. At the end of its first summer, after germination from a seed, a tree seedling is composed of one annual growth increment or growth layer. This somewhat cone-shaped increment, a fraction of a centimeter in diameter and only a few centimeters high, will not grow or change dimensions after the year in which it was formed, but will remain the same size and in the same position as long as the tree exists.

During the second year, another annual growth increment is formed around and above the first year's increment. At the end of the third year, an increment has been formed around that of the second year, and similar cones of growth are formed in each succeeding year. The growth increment of each year thus increases the diameter and height of the tree trunk.  

Most intriguing, it also has this diagram: 

Figure from page 7 of "Tree Rings" (1993) 

Which shows pretty clearly that the correct model of tree rings is that of stacked cones.  (And is pretty similar to my hand-drawn sketch above.)  

But... just to be sure, I wanted a verification check. So, I also did a search in Google Scholar for papers on this topic.  There, my search was much shorter and to the point: 

     [ cross-section tree height ] 

That led me pretty quickly to a technical paper "Two models for predicting the number of annual rings in cross-sections of tree stems" published in the Scandinavian Journal of Forest Research (2007).  

I won't bore you with the details (it's a fun paper to read, but you have to be willing to read through the math), but the key insight for me was that one of the key parameters of the model is "Number of annual rings (cambial age) in cross-section at height h", which strongly suggests that the number of tree rings varies by height.  (Looking at the data in detail shows that it does.)  More support for the idea of "stacked cones" rather than a simple cylinder.  

  

2. If tree rings are the fingerprints of a tree, I know that cloned trees can have very different ring patterns, but what about humans?  Do identical twin humans have identical fingerprints, or not?  

This was a much simpler Challenge.  My query was much like Ramon's: 

     [ identical twins fingerprints ] 

which quickly leads to two articles from reputable sources.  Medline Plus and  Healthline both of which tell us that: 

The finer details of the patterns of skin ridges are influenced by other factors during fetal development, including substances taken during pregnancy and the environment inside the womb. These developmental factors cause each person’s dermatoglyphs to be different from everyone else’s. Even identical twins, who have the same DNA, have different fingerprints.

And there you have it: reputable source and a verification from a second reputable source.  

SearchResearch Lessons

1. Even simple questions can be difficult to answer.  I guess that's often the case (standard example, "why is the sky blue?" is tricky), but you'd think searching out the answer would be straightforward. As you see, this isn't always the case.  Here we had to dig into the Books and Scholar literature to get a decent answer. Which reminds me... 

2. (Once again) Don't trust the LLMs for answers to tough questions.  It's bad enough that both ChatGPT and Gemini/Bard got the answer fundamentally wrong, but the fact that Gemini gives different answers between the SERP and the regular chat interface should give you a clue that something's really weird here.  

I'll say it again:  Always verify. Always get a second source (and asking another LLM is NOT validating.)  

Keep Searching!  

SearchResearch Challenge (2/14/24): Are tree rings nested cones or cylinders?

 While walking through a forest... 

P/C Sevenstorm (from Pexels.com)

... of very tall trees, I was wondering how old the trees were.  Luckily, just around the next bend in the trail there was the stump of a tree.  I counted the rings and found that it was around 25 years old.  But then I saw another cross section of the tree, but much narrower and taken from much higher up on the trunk, a bit like this: 

THAT started me thinking about markers of growth.  As you know, each ring is 1 annual growth cycle.  The dark bands are usually made of smaller cells that grow close together when times are tough, while the light bands are larger cells, created when living conditions are much better. 

But is the number of rings the same at the bottom of the tree as at the top?  That is... 

1. Are the rings in a tree trunk arranged as a cone or as a collection of cylinders?  In other words, if you count the rings at the top of the tree, would you see the same number of rings as at the bottom?  (If they're stacked cones, you'd expect the number to be different--if they're cylinders, you'd expect them to be the same.)  How ARE the tree rings organized inside of the tree trunk? 

2. If tree rings are the fingerprints of a tree, I know that cloned trees can have very different ring patterns, but what about humans?  Do identical twin humans have identical fingerprints, or not?  

Can you work your SRS magic on these Challenges and let us know?  

As always, tell us what you found, and how you found it.  (And yes, you can use LLMs or anything that floats your boat, including asking your fingerprint specialist detective uncle.)  Just be sure to include the details of what you did, including any tools or resources... be they AI or human.  

Keep Searching!  

PSA: Do not believe citations created by Gemini (Bard)

 As you probably know, 

... I'm writing a book.  That means every day I'm looking things up, checking into the backstory so I can be sure that what I'm writing is accurate, up-to-the-minute, and full of the zesty and intriguing insider information that you've come to expect from SearchResearch.  

Today I was looking up the difference in behavior between the Eurasian Tree sparrow (Passer montanus) and the ordinary House sparrow (P. domesticus).  Oddly, it turns out that even though they're very similar, the Eurasian Tree sparrow has a much smaller range that the House sparrow.  (Buy the book when it comes out to learn why anyone might be interested in this strange-but-true fact.)  For two very similar birds, the question is obvious: Why?  

In the process of searching for the answer, I thought that I should give Gemini (Bard) a try.  So I posed this question to it: 

[ why have house sparrows expanded their range dramatically since being introduced into the US, while Eurasian tree sparrows have not?  They're so similar, you'd think they would expand at a similar rate. ] 

And it gave a reasonable answer.  At least it looks reasonable.  

So I asked it to give me me a few citations:  

[ can you suggest further reading in the scientific literature about the differences in range expansion?] 

No surprise, it gave me a set of reasonable looking titles of papers I should read.  In fact, these titles look great!  I need to read these articles, and what's even better, there are actual links to the articles.  

What could go wrong?  Here's what I saw (I added the red Xs):  

To start with, NONE of those papers actually exist.  That's a serious deal-breaker. 

Yes, I checked everywhere, but no, I could not find any of these papers in the scholarly literature or even the trash heap. They just don't exist.   

And those links?  They go to actual papers, but not the papers cited, and in three cases, the links went to papers that weren't about sparrows at all but about random other topics!  

Which brings up the basic question--if Gemini can't get the citations and links correct, should I really trust the answer it gave to my first question?  

My answer:  I'm not going to do so.  It seems drunk.  

Just for giggles, I gave the same questions to ChatGPT-4.  Its answer to the first question was very similar to Gemini's, but to its credit, when I asked for citations, it replied with a hedge, listing places I could go look on my own, but NOT giving any direct citations.  At least the journals are real journals.  (Yes, there is an journal called The Auk, it's been published since 1884).  

I thought that ChatGPT would take the day here, but then, at the end of its answer, it included this very odd suggestion: 

Did I read that right?  "... here are some hypothetical examples of articles or chapters... though these exact titles may not exist."  

Maybe that's helpful?  (It certainly suggests some key terms that might be useful in doing regular searches.) 

But "hypothetical examples"?  I'm not sure this is really much of an addition to my search task.  

My bottom line?  Don't trust Gemini to tell you any actual citations... it just makes stuff up. (And that, my friends, makes me very concerned about the quality of the summaries it makes to complex or subtle questions...)  

Keep searching!  Your SRS skills are still relevant!  

Answer: How can I get an AI to summarize a document?

So, in summary… 

Last week we asked an important question:  How can we use LLMs (and AI tools in general) to help summarize things that we'd like to read?  

As I said, I find that I spend roughly half of my research time just browsing, scanning, and reading—it’s what you need to do to understand a topic area enough to do real work. 

Will AI systems make the long, original documents into a shorter, more focused work, punchier crystals of knowledge?  Or will that tool end up blurring everything into mush?  That's our choice: beautiful crystals of insight or mushy oatmealy language.  

What did we find out?  

1. How well does your favorite bit of AI technology do at summarizing long texts?  What system do you like for summarizing, and why?  

Let me start by pointing out the obvious:  Creating a good summary is fairly hard.  

I could quote Woody Allen's quip about speed-reading the infamously lengthy Tolstoy novel War and Peace--"It's about Russia."  

That's a summary, but not a useful one.  (Likewise, summarizing Moby Dick as "It's about whales," also doesn't help anyone.)  

What makes for a good summary?  

Interestingly, there are oodles of testing systems that measure the performance of LLMs on various dimensions: Closed-book Open-domain question-answering, Reading Comprehension, Instruction Following, Fact-Checking... etc.  

One of those dimensions is "Summarization."   (Probably the best known of the LLM performance measurements is the Hallucinations Leaderboard by HuggingFace. You can click on it for today's measures on a bunch of different LLMs on a bunch of different dimensions.)  

Basically, these measures of the quality of a summarization look at the overall similarity between the text (usually texts that are between 200 - 4K words long) and the summary that's generated by the AI tool.  That is, if there's a high degree of overlap in the words used in the summary and the original text, then the score is high. (The most commonly used measure is the ROUGE score to measure summary/original similarity.)  

Of course, while the ROUGE score is handy and easy to compute, it's not necessarily what makes for a good summary.  If I summarize  Frankenstein as "an exploration of how a quest for understanding the secret of life, and how it all goes horribly wrong," that's not going to be ranked very highly by ROUGE.  

A good summary, like a good explanation, is largely determined by who the summary is for, not its term overlaps.  A good summary of War and Peace to a 10-year old kid is (or should be) very different than for a 25-year old graduate student in world literature.  Likewise, a summary of something very technical (say, Calculus: Early Transcendentals by James Stewart, probably the best-selling math textbook on calculus in English) would be very different depending on the target, but also what the purpose of the summary is.  Summaries can have very, very different uses.  A summary of a book for the New York Times Book Review (which is intended to give a critical perspective on the text) will be different from a review that you post on GoodReads.com (which usually gives the plot points and description).  

Having said all of that, what DO people like as a summarization tool?  (I'm assuming we're not going to use human-written summaries, such as Blinkist, Sparknotes, or Cliffnotes.)  

The bigger question is actually "what LLM will actually summarize long texts?"  

2. Test out your summarization method on two long-form texts.  First, let’s try that classic gothic tale, Frankenstein by Mary Shelley.  (Here’s a link to the full text that you can use.) How good is that summary?  

As I'm sure you found out, there's no convenient way to upload a long text file into Bard/Gemini. If you paste the entire text of Frankenstein into Bard, it stops accepting input around page 15.  This is obviously a problem. 

If you upload the full-text of Frankenstein into ChatGPT4, it not only uploads easily, but if you then ask for a summary, it produces a very nice one.  This is the ChatGPT4 summary of Frankenstein: 

The novel "Frankenstein" by Mary Shelley begins with letters from an explorer named Robert Walton to his sister, where he describes his journey to the North Pole. During this expedition, Walton encounters Victor Frankenstein, who then narrates his own tragic story of ambition, creation, and loss. Victor, a young scientist, creates a sentient creature in an experiment, but is horrified by his creation and abandons it. The creature, seeking companionship and understanding, faces rejection and becomes vengeful, leading to tragic consequences for both creator and creation. The novel explores themes of ambition, isolation, responsibility, and the quest for knowledge.

If you ask for a longer summary (which I did), it creates a slightly longer version, but only about 100 words longer.  I couldn't figure out how to get it to create a much longer version. (Even when I asked for 1000 words, it topped out at 400.)  

So, for summarizing long texts, ChatGPT4 wins over Bard by a monstrous amount.  

3. Second, let’s try your summarization method on a piece of text you might have read, but might have slightly forgotten—Chapter 10 of my book, The Joy of Search, link to the full-text of Chapter 10 here.  "When was oil first discovered in California?"  Did your summary method create a good/useful summary?  

This was really interesting: I got both ChatGPT4 and Bard/Gemini to produce good summaries of Chapter 10 of The Joy of Search.  Let's look at their summaries side-by-side.  

First, here's Bard/Gemini's summary: 

Bard/Gemini: 

Summary of the Text on California Oil Discovery:

The text explores the complexities of discovering when and where oil was first found in California. It emphasizes the importance of critical thinking and careful research when navigating historical information.

Key Points:

• Multiple Claims: Different sources make various claims about "first" oil discoveries, citing events like:
  • 1865: Union Matolle Company's commercial sale from Humboldt County.
  • 1876: Pico No. 4 well producing continuously for over a century.
  • 1892: Edward Doheny's supposed oil strike using a eucalyptus trunk (less credible).
  • 1855: Andreas Pico's small-scale distillation for local use.
• Challenges in Research:
  • Unreliable sources and repetition of errors, especially online.
  • Conflicting interests and "romantic wildcatter" narratives influencing storytelling.
• Best Answer:
  • For commercial sales, evidence points to the Union Matolle Company in 1865.
  • For long-term success and impact, Pico No. 4 in 1876 holds the title.
• Research Lessons:
  • Define your question clearly.
  • Be wary of duplicated content and unattributed citations.
  • Organize your findings and compare competing claims with evidence.

Additional Notes:

• The text criticizes poor scholarship and plagiarized content.
• It emphasizes the importance of scrutinizing sources and understanding potential biases.
• The provided research tips can be applied to various historical inquiries.

This summary captures the main points of the text while highlighting its critical approach to historical research.

And here's ChatGPT4's summary: 

ChatGPT4:

The text is a research narrative exploring the origins of oil discovery in California. It begins with the author's personal reflection on growing up in Los Angeles, an area dotted with oil wells, which sparked the question: When and where was oil first discovered in California?

The author's search for an answer reveals complexities due to conflicting information and widespread text reuse across sources. The narrative follows the investigation through various claims:

1. 1. Union Matolle Company in 1865: Said to be the first productive well in California's Central Valley, but the location was inaccurately attributed, as the company operated in Humboldt County, not the Central Valley.

2. 
   

3. 2. Charles Alexander Mentry in 1876: Credited with striking oil in Pico No. 4, which became California's first commercially successful well, corroborated by Chevron's corporate history and a Wikipedia entry.

4. 
   

5. 3. Edward Doheny in 1892: Reported to have used a eucalyptus tree trunk to drill for oil in downtown LA, but the narrative casts doubt on this claim due to its tall-tale nature.

6. 
   

7. 4. Andreas Pico in 1855: Known for distilling small amounts of oil in Pico Canyon, but not considered a commercial success.

The author finds that the Union Matolle Company had the first commercial sales of refined oil from a well in Humboldt County in 1865, but Pico No. 4, beginning operations in 1876, had the most enduring success. The narrative concludes with insights on research methodology, emphasizing the importance of precise questions, skepticism toward duplicated content, and the organization of findings to answer complex research questions.

Both are decent summaries, but there's an interesting difference between them.  ChatGPT4's summary is primarily focused on the oil discovery claims (that's what the 4 points are all about).  

By contrast, Bard/Gemini's summary is focused on what makes this online research difficult to do, and the lessons you should learn along the way. (That's what Bard's bullet points highlight.) 

To be sure, they both mention that this chapter is about research methods and skills... but I think Bard/Gemini gets the focus a bit more right than ChatGPT4.   

SearchResearch Lessons

1. As we've learned before, different tools have different strengths.  ChatGPT4 is MUCH more able to handle large quantities of information (we could upload Frankenstein to ChatGPT4 but not to Bard).  You, the SearchResearcher need to understand what you can do with each tool. 

2. Summaries are complicated--ask for exactly the kind of summary you need.  For instance, I could have asked for a summary of Chapter 10 "written for a 6th grader" and the language and lessons would have been much simpler.  

I'm sure I'll have more to say about this topic in days to come.  But for the moment, different LLMs have different strengths.  Try them all! 

Keep searching! 

Interlude: Two SRS-style stories and the regretted loss of cache:

 It's been busy here at the SRS rancho... 

Search interlude. P/C DallE-3. 

... and so today is an interlude with a few stories you'll want to read.  

1.  First up, a story by Latif Nasser of RadioLab (the brilliant podcast) about his research quest.  In a longish Twitter/X thread, he tells the story of how he noticed a small, just slightly wrong detail in his young son's poster of the Solar System.  He noticed a moon orbiting Venus that was labeled "Zoozve."  A quick search told him that, as he thought, Venus doesn't have any moons.  He then "... googled “Zoozve” and got no results, literally zero results in English. Only results were in Czech and they were about zoos. Not what I was looking for." 

Close up of the original Solar System poster by Alex Foster.

After calling a NASA friend (Liz) and learning the same thing (yeah--no moons around Venus), he contacted the artist directly (Alex Foster), who said that he saw it on a list of moons... but he couldn't find that list any longer. 

Then, in a dramatic turn of events, Liz, the NASA friend called back saying "I think I figured it out."  Turns out there IS an object near Venus called "2002-VE"... could the artist have misread this as "Zoozve"?  

To be sure, 2002-VE isn't a moon, it's more of a wandering asteroid--a big rock that's currently orbiting Venus. Maybe you can call it a moonlet, or the more technical term, a quasi-satellite.    

Latif then called Brian Skiff at Lowell Observatory in Arizona--he's the guy who found it in 2002 as part of the LONEOS project--a very large-scale asteroid hunt for asteriods near Earth than could potentially smack into our planet causing a terminal event.

Along the way, Latif also found 2 astronomers who kept watching 2002-VE: Seppo Mikkola in Finland and Paul Wiegert in Canada. They told him that Zoozve is NOT a moon of Venus. But it’s also NOT really a moon of Venus. It’s both of Venus and not of Venus. 

A little more digging led Latif to a paper published in the Monthly Notices of the Royal Astronomical Society.   In their paper Asteroid 2002 VE68, a quasi-satellite of Venus, the authors point out that this moonlet has been in orbit around Venus for around 7,000 years, and will probably leave that orbit in 500 years (or so) until it's captured by another planet, or just wanders around the sun.  

As they write in the paper, "From the evolution of the orbit of this object, we conclude that it may have been a near-Earth asteroid, which, some 7000 yr ago, was injected into its present orbit by the action of the Earth."  

Latif then went on to learn that these quasi-satellites are complicated beasts, following extraordinarily complex orbits, and sometimes (as in the case of 2002-VE) moving their orbits between planets.  

SearchResearch Lessons:  

I love Latif's story here: it all started when he noticed a small detail that didn't fit in with what he knew ("there's no moon around Venus!"), so he started a research project to figure out what was going on.  I like that he failed in his Google search, but he kept at it, even contacting the artist and an astronomically learned friend.  

Liz, the NASA friend, had the key insight--maybe this was a misreading of something very similar!  Once you had the correct name for the thing, search gets a lot simpler.  

Bravo!  

(Postscript: Latif and Brian Skiff proposed that the quasi-satellite be called Zoozve... and the International Astronomical Union’s Working Group for Small Bodies Nomenclature (who keeps track of these things), ended up adopting the name, thereby making Alex Foster's poster correct retroactively.  Link to the paper that officially adopted the name.)  

Official announcement in the IAU's working group

2.  A story by Henk van Ess: Research into why planes sometimes travel faster than expected

On a recent flight, Friend-of-SRS Henk van Ess was puzzled: why did the flight's arrival time show as a full hour ahead of schedule?  What would cause that to happen?  

In his blog post at DigitalDigging.org (which I recommend to you), he gets to the bottom of this question through a conversation with ChatGPT and some sharp reasoning to determine that biggest factors for the faster times are:  (a) it's not tailwinds; (b) it's not the jet stream; (c) it's not having a light load with fewer passengers onboard.  

It IS primarily due to buffer times built into their schedule.  (But they did have a lack of headwinds, which also helped.) 

But his article points out that there's a big difference between ChatGPT 3.5 and ChatGPT 4 with the Data Analyst option turned on.  Your choice of LLMs really matter--understand which one you're using and be aware of the differences. 

SearchResearch Lessons:  In the end, Henk says that "... if you don't ask the right questions, you won't get the answers you need. Being clear and specific is key."  

We've talked about exactly this point many times here on SRS.  Understand your tools and be clear--very clear--about what you're asking.  

3. The loss of the cache:  

Most SRS Readers know that the cache: operator lets you pull up the last cached version of a web page.  (See the SRS discussion of cache: from 2018.)  

Alas, Google has deprecated this feature, so we can't use it any longer. (See Danny Sullivan's Twitter post about this.) 

In the meantime, I HIGHLY recommend that you get the browser Wayback Machine extension for your preferred browser.  Here's the list: 

     Chrome Wayback Browser Extension 

     Safari Wayback Browser Extension 

     Firefox Wayback Browser Extension 

     Edge Wayback Browser Extension 

Note that Bing still supports the cache: operator, so you don't really need it if you're an Edge user.  

FWIW, I suspect more features will be deprecated in the future, but I don't know what / when / or why.  It's just gonna happen as Google tries to save money and reduce the overall complexity of the search system from their side (and, presumably, invest those savings into Bard, or whatever they're going to call their GenAI LLM).  

SearchResearch Lessons:  Things change... even operators.  Stay tuned because this will continue to happen.   

Back to our regular program tomorrow with an answer to the "How to summarize" Challenge from the previous post. 

Keep searching!